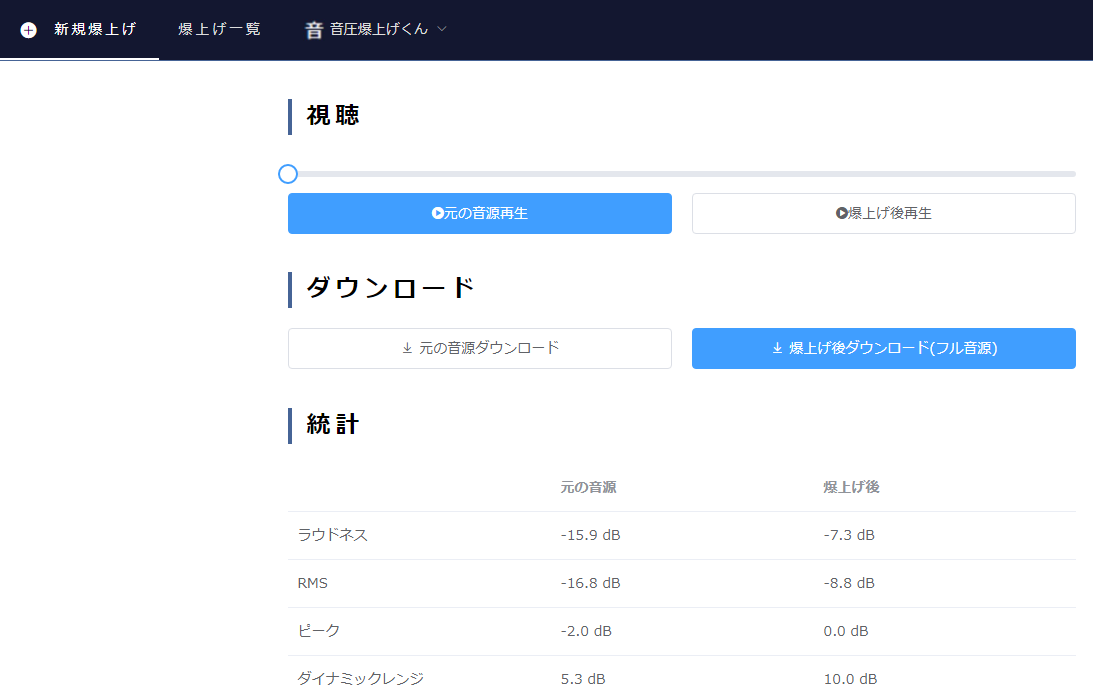
音圧を上げるためには熟練したミックスとマスタリングの技術が必要ですが、今すぐ音圧を上げたい方や、音楽そのものに力を注ぎたい方にとって、手軽に音圧を上げられるツールが音圧爆上げくんです。
自動でマスタリング
※ 推奨ブラウザ: Chrome
音圧爆上げくんとは?
全てのDTM作曲家に送る・・・
好きな音源を、ワンタッチで、大きい音にできるウェブツール!
新しいマキシマイザーです。
特徴
1.プロ並みに音圧を上げられる!

2.好きな音質に近づけられる!
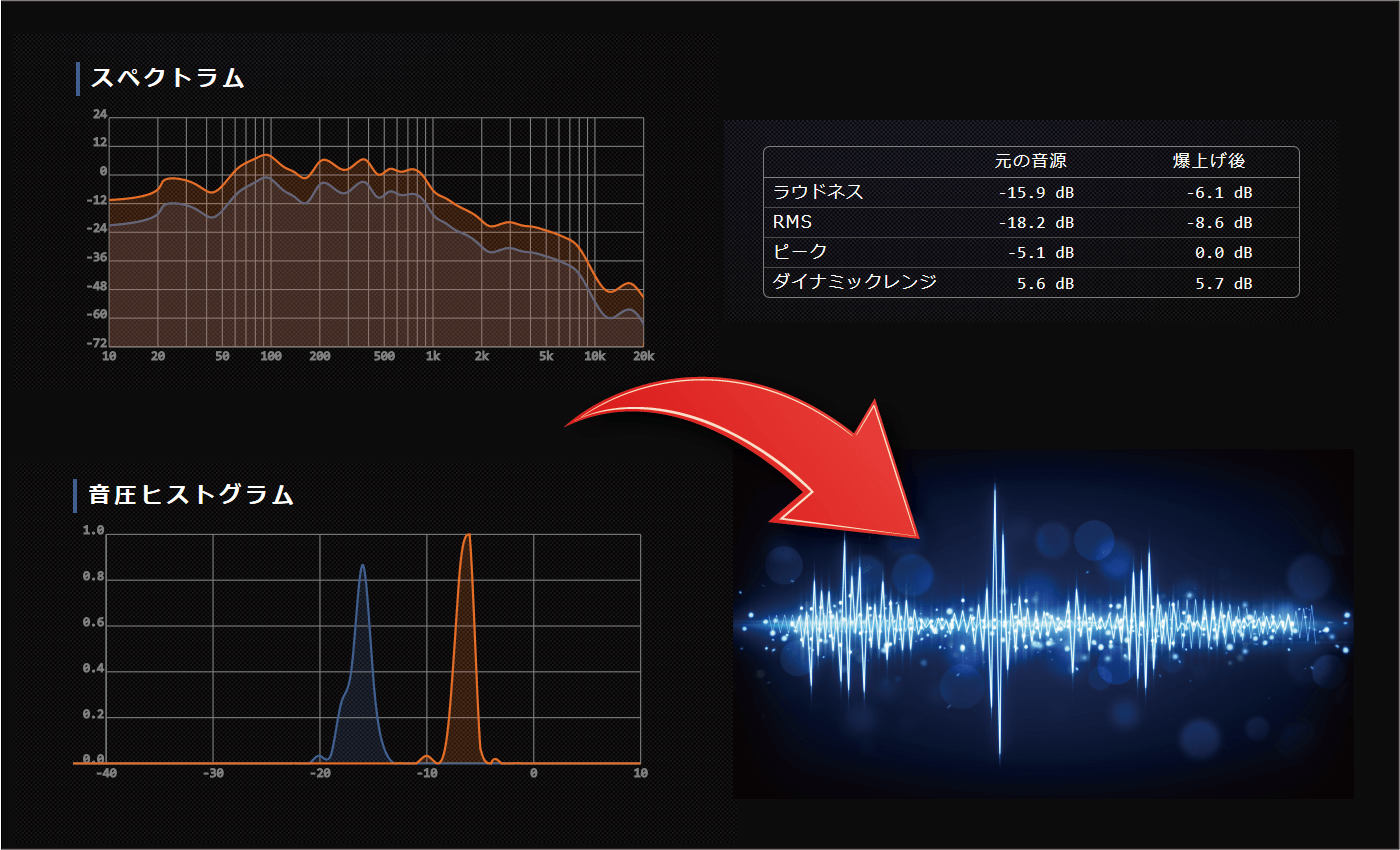
LANDRなどと同様、自動オンラインマスタリング機能を搭載しています。音圧爆上げくんの特徴は、リファレンス音源を指定できることです。好きなアーティストの音源や、気に入った音質の音源をリファレンスとして指定することで、ワンタッチで好きな音質に近づけられます。
3.無料!

以前は有料でしたが、現在は、全て無料です。
デモ音源
2.比較方法
比較用の音源を、音圧爆上げくん、FabfilterのPro-L、WavesのL3-16で圧縮しました。音圧爆上げくんは自動マスタリングをオフに設定しています。リミッターの設定は、ラウドネスがリミッター間でだいたいそろうように各リミッターのゲインを調節しました。ゲイン以外の設定は起動時のデフォルト設定を用いています。 DAWのサンプリングレート設定は44.1kHz、書き出しフォーマットはステレオ 44.1kHz 24bit wavです。